The purpose of LOKI97:
It was intended to be an
evolution of the earlier LOKI89 and LOKI91 block
ciphers. And then use 128-bit data and 128/192/256 bit keys, with a greatly
strengthened key schedule, and using a significantly more complex round
function composed of 2 S-P layers.
About:
LOKI97 is block cipher with
128-bit data and a 256-bit key schedule, which can be initialised by 128, 192,
or 256-bit keys. The data computation uses 16 rounds of a balanced feistel
network with a complex function f which incorporates two S-P layers. The
256-bit key schedule uses 48 rounds of an unbalanced feistel network using the
same complex function f to generate the subkeys.
how it Works:
LOKI97 encrypts a 128-bit
plaintext block to create a 128-bit ciphertext block. The data computation is
initialised by dividing the 128-bit plaintext input value [L|R] into
two 64-bit words:
L0 = L
R0 = R
These are then processed
through 16 rounds (i=1,16) of a balanced feistel network:
Ri = Li-1 xor f(Ri-1+SK3i-2,SK3i-1)
Li = Ri-1+SK3i-2+SK3i
Each round uses both XOR
(additional modulo 2) and integer addition (modulo 264) of the 64-bit data values.
Since these are from incompatible groups, the operations do not compose, and
thus strengthen the rounds against attacks, as well as obscuring the final
round input value at the output, and providing some additional diffusion of
input bits.
The resulting 128-bit
ciphertext output value is composed of:
[R16|L16]
The function f(A,B) should
be designed to ensure maximal avalanche between all input bits to the function.
The current proposal for this function f(A,B) is
given below.
The decryption computation
involves splitting the ciphertext into two 64-bit words:
L16 = L
R16 = R
and then running the rounds
in reverse. ie: use 16 rounds (i=16,1)
Ri-1 = Li xor f(Ri-SK3i,SK3i-1)
Li-1 = Ri-SK3i-SK3i-2
The 128-bit plaintext value
is given by
[R0|L0]
The overall data computation
thus looks as follows:
Key Schedule
LOKI97 uses a key schedule
based on an unbalanced Feistel network (as per Schneier and Kelsey [ScKe96]),
operating on four 64-bit words. It using the same function f(A,B) as
the data computation to provide sufficient non-linearity to ensure that
computing related keys is difficult.
The key schedule is
initialised, based on the size of the key supplied, into the four 64-bit words [K40|K30|K20|K10] as
follows:
Given a 256-bit key [Ka|Kb|Kc|Kd],
let
[K40|K30|K20|K10] = [Ka|Kb|Kc|Kd]
Given a 192-bit key [Ka|Kb|Kc],
let
[K40|K30|K20|K10] = [Ka|Kb|Kc|f(Ka,Kb)]
Given a 128-bit key [Ka|Kb],
let
[K40|K30|K20|K10] = [Ka|Kb|f(Kb,Ka)|f(Ka,Kb)]
These are then processed
through 48 rounds (i=1,48) to compute the 48 subkeys SKi as
follows:
SKi = K1i = K4i-1 xor gi(K1i-1,K3i-1,K2i-1)
K4i = K3i-1
K3i = K2i-1
K2i = K1i-1
where:
gi(K1,K3,K2)=f(K1+K3+(Delta*i),K2)
Delta = (sqrt(5)-1)*263 =
9E3779B97F4A7C1516
Three rounds of the key
schedule are required to produce the three subkeys for each round of the data
computation. Thus a total of 48 rounds are required for the key schedule, for a
cost of approx three encryption computations.
The integer addition (module
264) of K1+K3+(Delta*i) forms an incompatible group with the xor used
on the previous round output, as in the data computation. It includes multiples mod
264 of Delta, a value derived from the golden ratio, to reduce
symmetry problems.
Decryption uses the keys in
reverse order with (additive) inverses of the SK3i-2 and SK3i subkeys.
These will need to be precomputed in encrypt order first - there is no reverse
shortcut as for LOKI89 and LOKI91.
Function f(A,B)
The highly non-linear
function f(A,B) takes two 64-bit input values A and B, processes them
using two layers of S-boxes with the highest possible non-linearity, to produce
a 64-bit output. The two permutations are used to ensure maximal avalanche
between all bits in the function.
The major novel feature in my
proposed design is the use of two layers of the S-P network instead of the one
used in most other current feistel ciphers. This is to provide the desired
maximal avalanche, as well as to minimise the posibility of suitable
differential or linear characteristics. The presence of the keyed permutation
on the input of the function, switching between different S-box inputs, ensures
that predicting which S-box a particular input bit goes to is difficult. This
increases the difficulty of deriving any useful attack characteristics.
This function is specified as
follows:
f(A,B) = Sb(P(Sa(E(KP(A,B)))),B)
Graphically, it looks as
follows:
In more detail, the various
component operations used are:
KP()
a very simple keyed
permutation which splits its 64-bit input A into two 32-bit words, and uses the
lower (rightmost) 32-bits of input B to decide whether to exchange
corresponding pairs of bits in these words (if key bit is 1), or not (if key
bit is 0), similar to that used in ICE [Kwan97].
It may be computed as:
KP([Al|Ar],SKr) = [((Al &
~SKr)|(Ar & SKr)) | ((Ar & ~SKr)|(Al & SKr))]
E()
expansion function, similar
to LOKI91 but shifted for easier implementation, which selects overlapping
groups of 13 bits (S1) or 11 bits (S2), so that at least some bits influence 2
S-boxes simultaneously, and with the preceeding addition, means all bits have
some influence on multiple S-boxes. E thus maps a 64 bit input value [63-0] to
a 96 bit output value [4-0,63-56|58-48|52-40|42-32|34-24|28-16|18-8|12-0].
Sa(), Sb()
are two columns of S-boxes,
composed by concatenating boxes S1 and S2 (specified below),
with Sa()=[S1,S2,S1,S2,S2,S1,S2,S1], and Sb()=[S2,S2,S1,S1,S2,S2,S1,S1]. In
Sa() the inputs are autoclave (input+key from the output of E), in Sb() the
upper bits are pure key bits (from the lower,rightmost 32-bits of B).
P()
permutation to diffuse S-Box
outputs across full 64-bit width, using a regular, latin-square, pattern,
similar to LOKI91, but with a slight change so the same output never goes to
the corresponding input. P maps input bits [63-0] to
[56,48,40,32,24,16,08,00,57,49,41,33,25,17,09,01,
58,50,42,34,26,18,10,02,59,51,43,35,27,19,11,03,
60,52,44,36,28,20,12,04,61,53,45,37,29,21,13,05,
62,54,46,38,30,22,14,06,63,55,47,39,31,23,15,07]
This function can
theoretically be implemented with 24 table lookups (8 each
for Sa, P, and Sb), plus some
and’s, or’s, xor’s, shifts and adds for each round, mak-ing it reasonably fast
and efficient. Using compiled code of course wont achieve
this ideal.
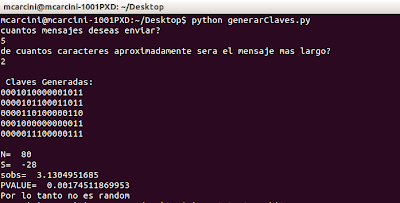
Example:
For do this example i use the
next page:
this page is just for the
algorithm LOKI97 but there is other where you can do it with different algorithms
and modes:
In this case i use de mode: Electronic
codebook (ECB)
The simplest of the
encryption modes is the electronic codebook (ECB) mode. The message is divided
into blocks and each block is encrypted separately.
plain text : this homework is
for Cryptography
Key : This is a very secret
key
After of Encrypt i get the cipher
text:
amCKLPRri8TC0M8EjY6D+O0g+Apxum2iY//NPobY/7JJFtxLcn64UKZUvgtjNScT
and i get the plain text with the key and cipher text:
plain text : this homework is
for Cryptography
attacks and vulnerabilities:
resistant to differential
attacks
resistant to linear attacks